Our website uses cookies to enhance your browsing experience.
A list is a linear collection of data that allows you to efficiently insert and delete elements from any point in the list.
A list consists of nodes. Each node contains data and a pointer to the next node. If a node has a pointer only to the next node in line, it is a singly linked list. Schematically, it may look like this:
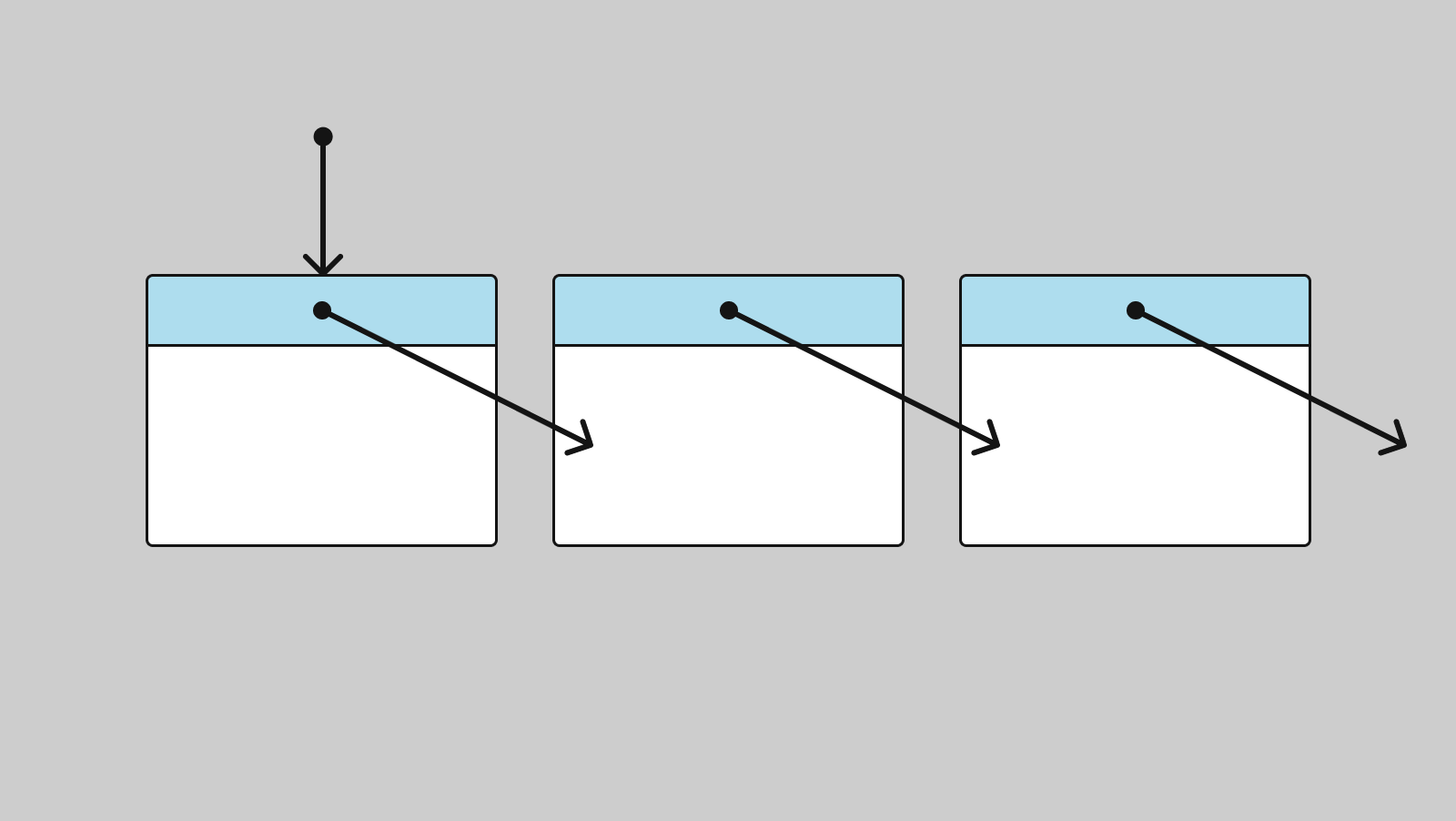
In the singly linked list, the pointer of the last node to the next one is null. This way, the list is just a pointer to the first node.
Here you can find an example of a singly linked list implementation in C, and here is an example for C++.
A node can have a pointer to the next node as well as a pointer to the previous one. This kind of list is called doubly linked. Schematically, it looks like this:
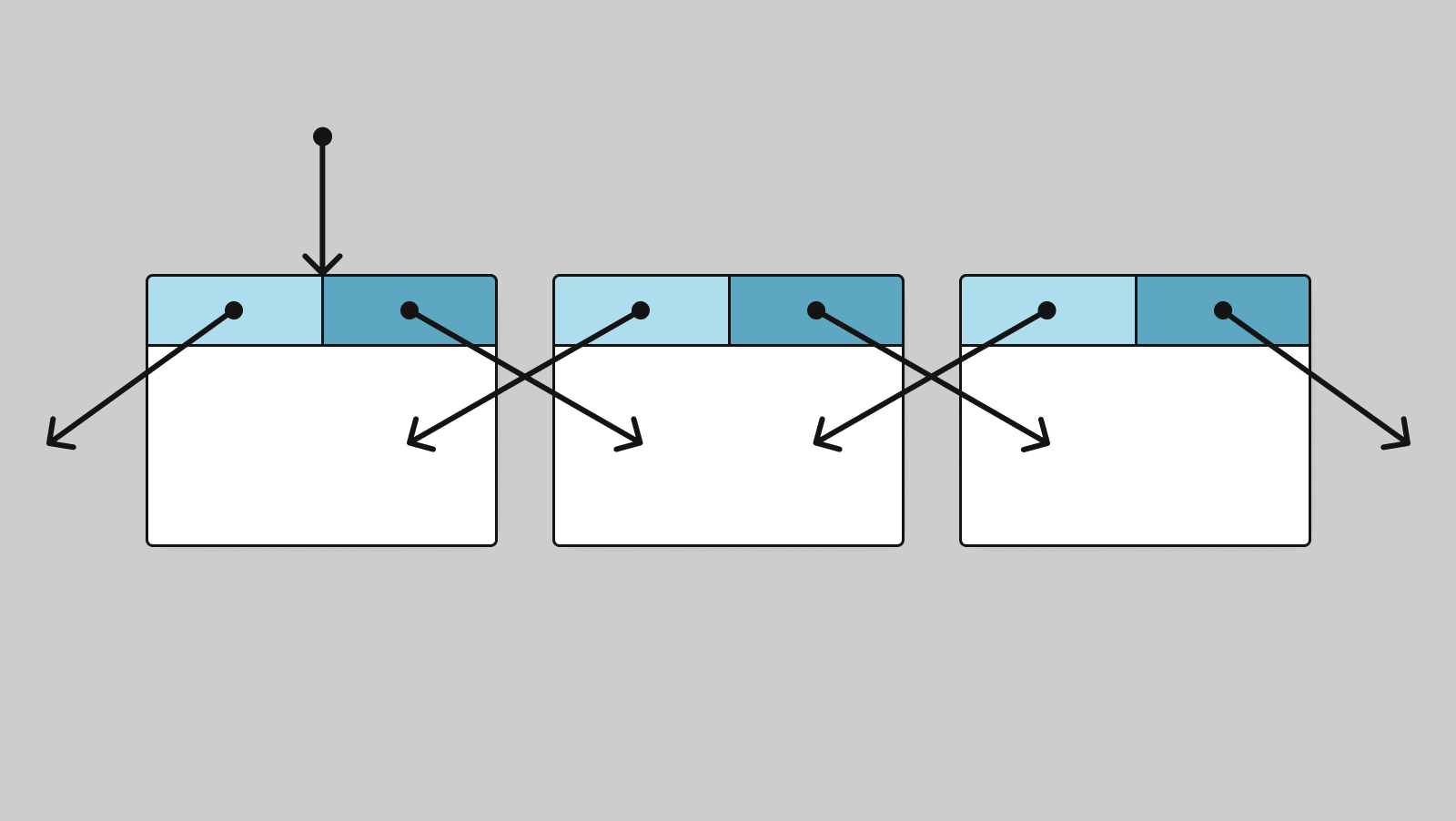
In the doubly linked list, the pointer of the first node to the previous one is null.
Here you can find an example of a doubly linked list implementation in C, and here is an example for C++.
To traverse the list, store the pointer to the current node. You can traverse to the next node by the pointer stored in the current node.
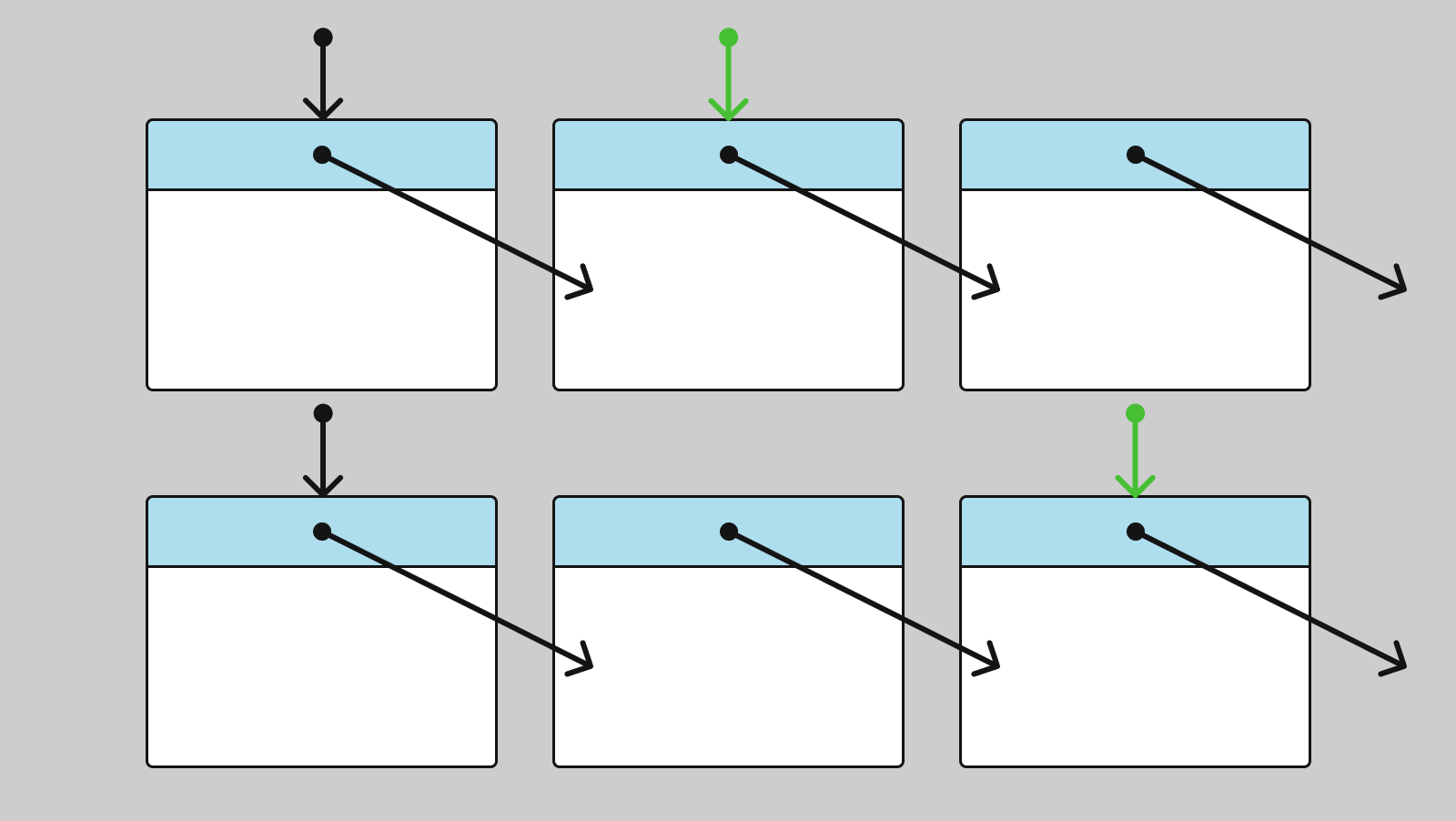
To access the nth element of the list, you need to sequentially traverse the first n nodes by their pointers to the next node. As a result, an arbitrary element is accessed in O(n) time.
If you need to find an element in the list, traverse it and check each node for the target element. In the worst case, if the item needed is not there, you will traverse the entire list. In the general case, the search is performed in O(n) time.
Inserting elements at the list is performed in O(1) time. To insert an element at the list, create a new node and update several pointers' values.
To insert a new node into a singly linked list, follow these steps:
Schematically, the insertion looks like this:
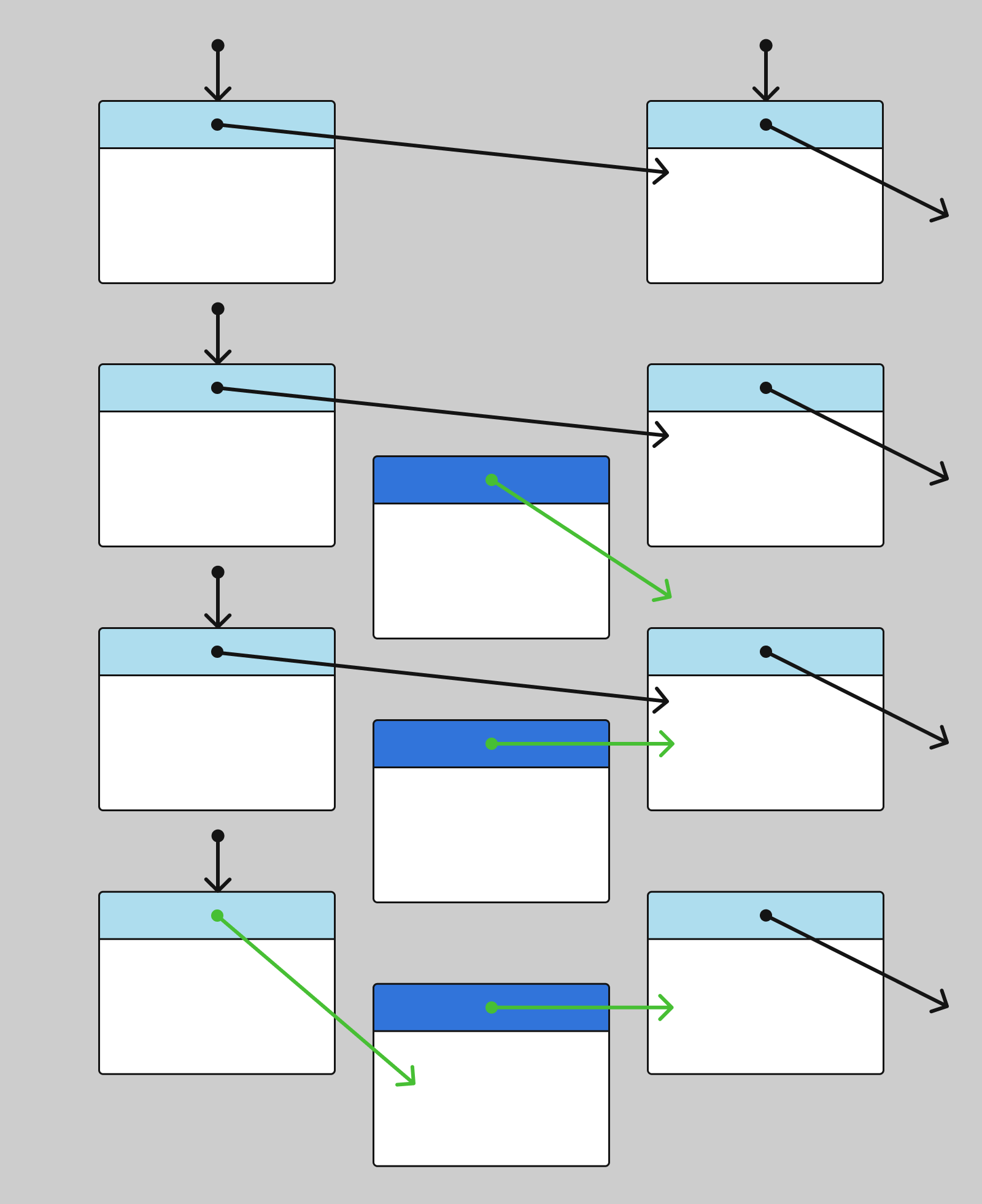
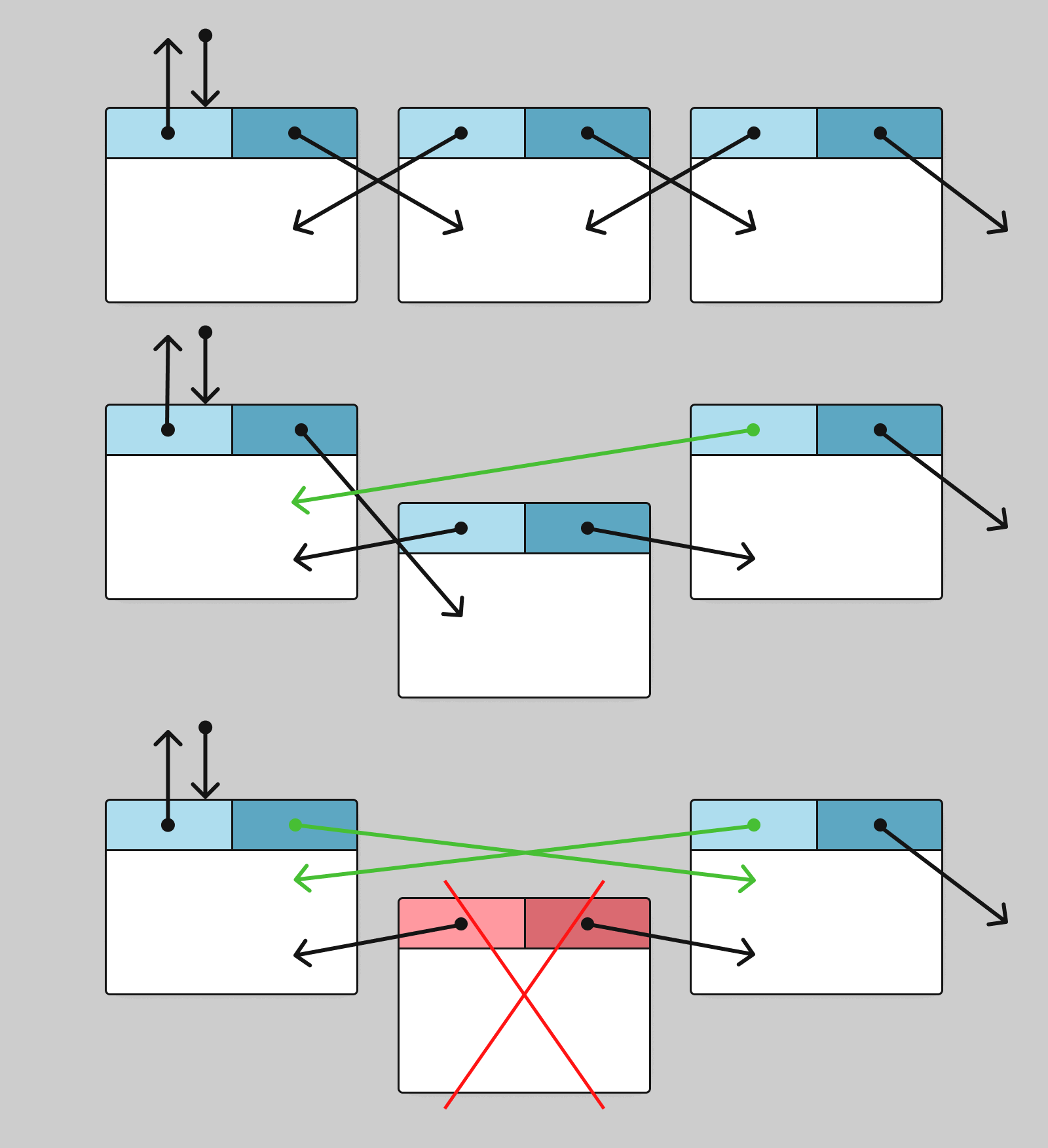
To insert a new node into a doubly linked list, follow these steps:
Schematically, it looks like this:
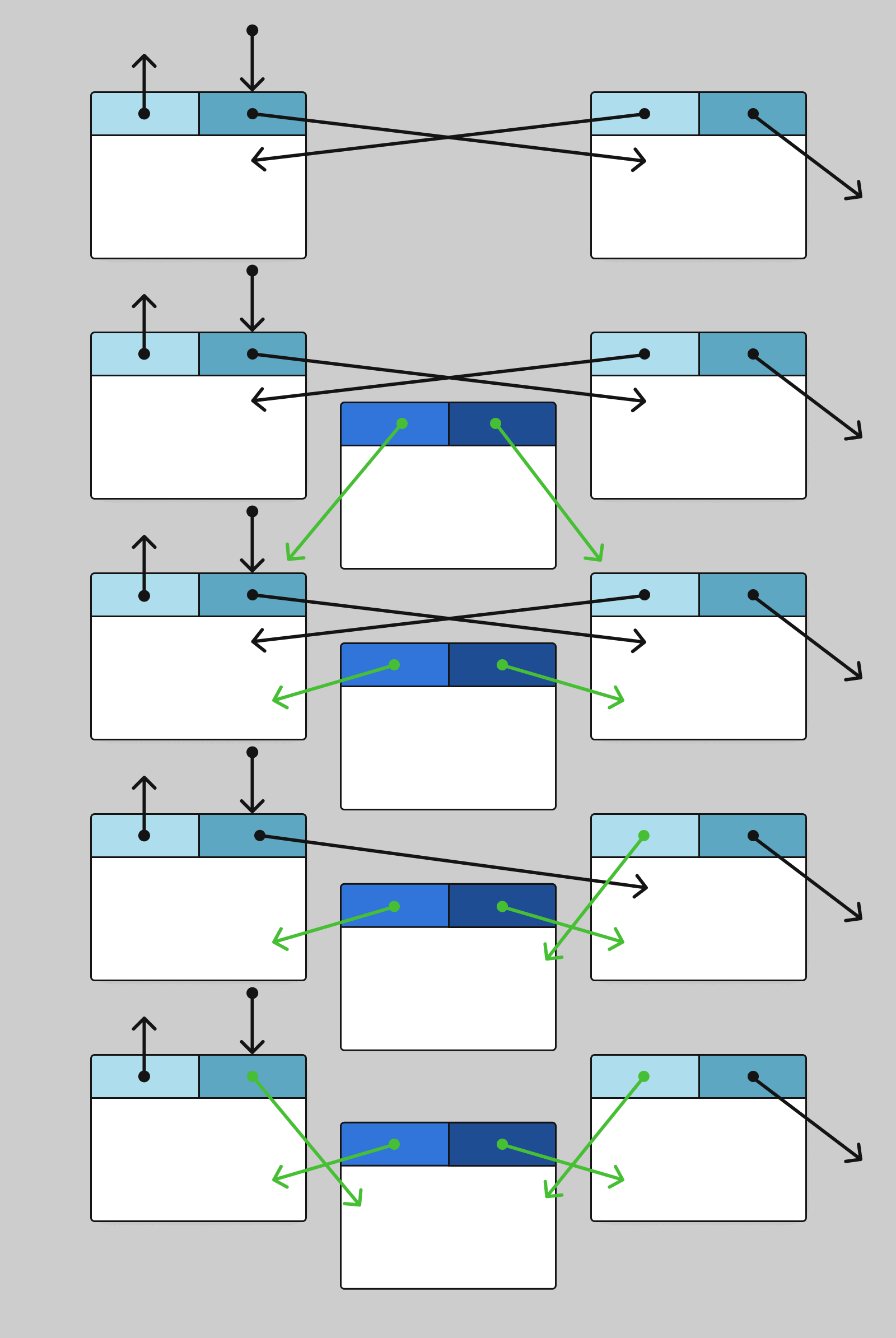
Deletion from a list is performed in O(1) time. To remove a node from the list, update several pointers.
To delete a node in a singly linked list, follow these steps:
Schematically, it looks like this:
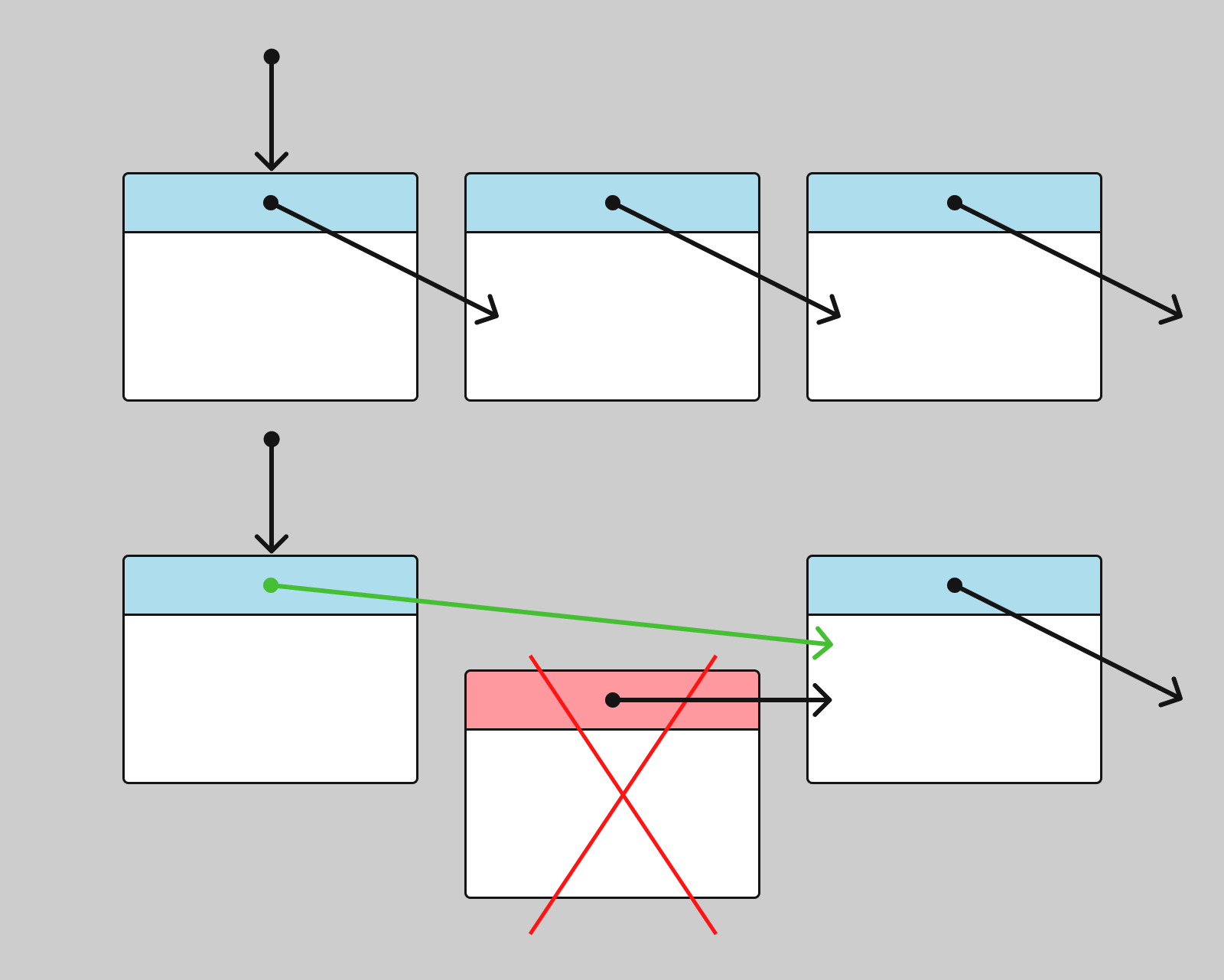
To delete a node in a doubly linked list, follow these steps:
Schematically, the deletion looks like this:
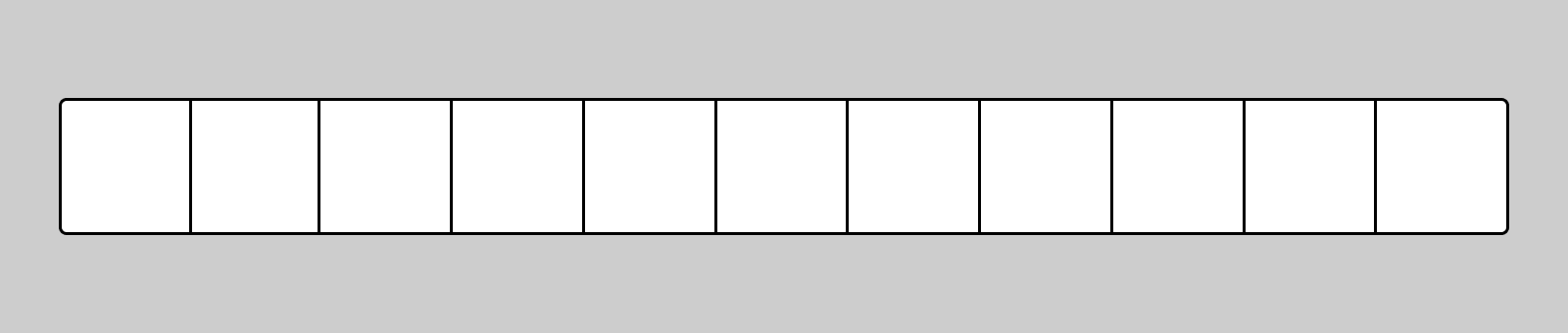
An array is a linear data structure that continuously stores elements in memory and supports accessing an arbitrary element of a sequence. Schematically, an array looks like this:
To remove an element from the middle of an array, you need to move all the elements after the element you want to remove one position forward:
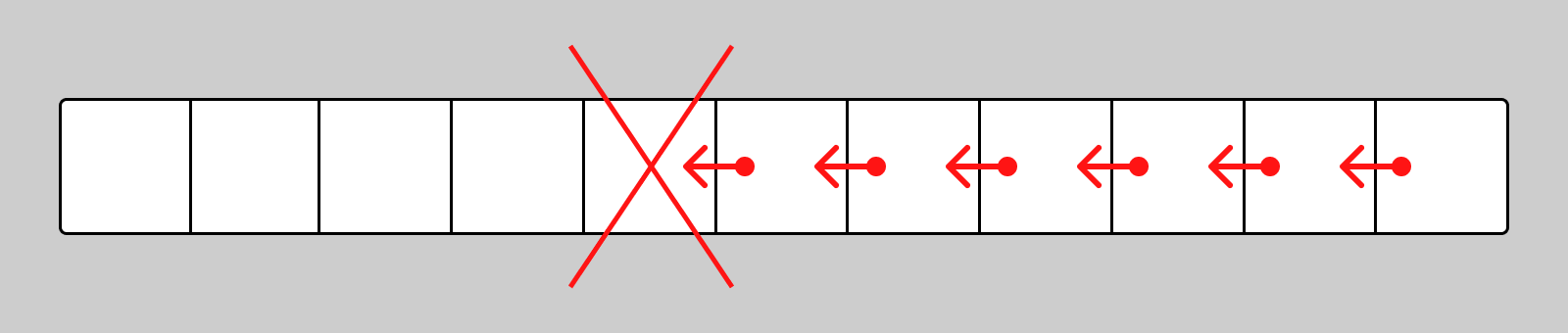
To delete the 100th element in an array of 1000 elements, you need to make 900 moves. Thus, it takes O(n) to remove an element from any position except the end. Removing an element from the end takes O(1).
Inserting an element in the middle of an array is no easier. In this case, all array elements after the insertion point need to be moved one position back:
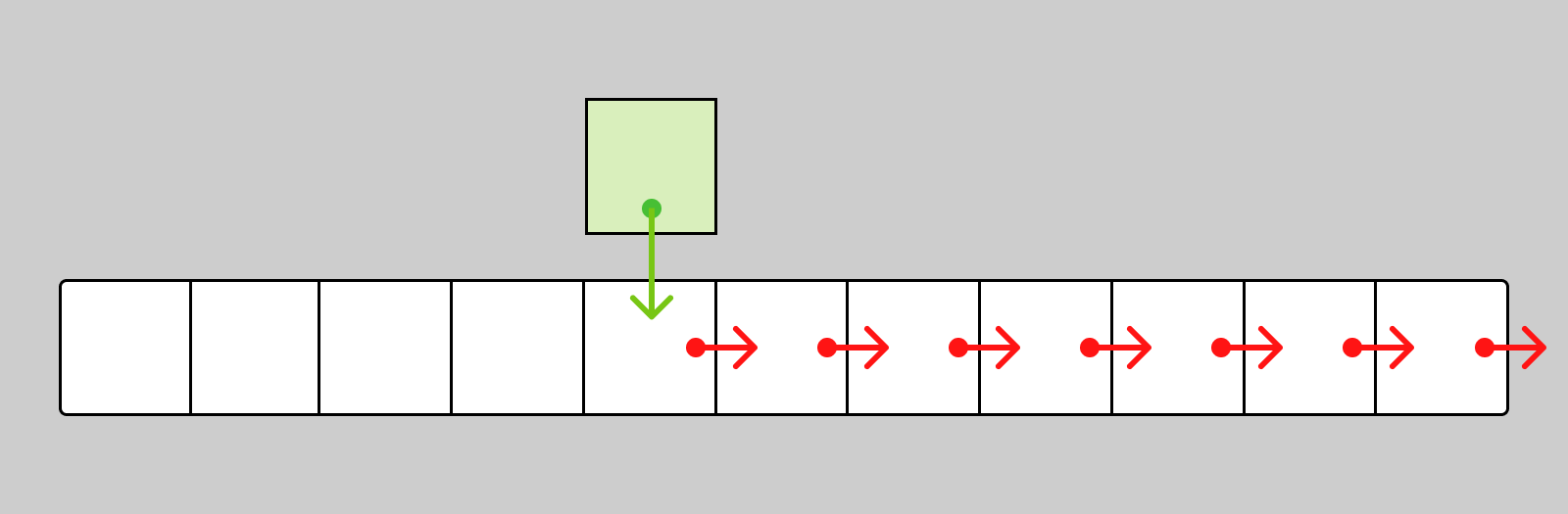
To insert an element at the 100th position in an array of 1000 elements, 900 moves are needed. Thus, it takes O(n) to insert an element at any position except the end. Inserting an element at the end takes O(1).
As we can see, the only efficient place for inserting and deleting elements is the end of an array. At the same time, updating several pointers (four or less) is enough to insert or delete an element anywhere in the list. If you need to delete and insert elements in arbitrary places of the sequence, then it is better to store them in a list.
Based on the above, we can highlight another advantage of lists: they ensure that references to elements and iterators to nodes remain valid during any insertions and deletions (except for the nodes being deleted). Things are more complicated when it comes to arrays:
The disadvantage of lists is the slow access to an arbitrary list element. If you need the 901st list element, you will have to traverse all 900 other list elements. In addition, list elements are usually arranged inconsistently in virtual memory. This means that each move to the next node will be accompanied by an arbitrary memory access.
Array elements are located continuously in virtual memory. Therefore, an access to an arbitrary element is a single access to the address obtained using address arithmetic: an offset equal to n * sizeof(Item) is added to the zero element address. Moreover, if small array elements are accessed sequentially, modern processors recognize this and load data in advance into cache (cache prefetching). For example, when accessing an int array element with a size of 4 bytes, if a cache line has a size of 64 bytes, the processor will load 16 elements into its cache at once. In case of lists, cache misses cause the processor to access virtual memory more often. This is much slower than CPU cache accesses.
Therefore, if you need random access to sequence elements, use an array instead of a list.
A brief comparison of an array and a list:
|
Accessing an arbitrary element |
Inserting a new element |
Deleting an arbitrary element |
|
|---|---|---|---|
|
Array |
O(1) |
O(n) in the general case O(1) when inserting at the end |
O(n) O(1) when deleting from the end |
|
List |
O(n) |
O(1) |
O(1) |
0
0
0
Your message has been sent. We will email you at
If you do not see the email in your inbox, please check if it is filtered to one of the following folders:
303
0
0