Have you ever wondered if you could fully write code using only the #define directive in C? It's well-known that the C++ templates are Turing-complete—developers write ray tracers that do all evaluations at compile time (instead of runtime). What about the C preprocessor? As it turns out, the question is a bit more complex than we first thought.
To manage expectations, there won't be any ray tracers, but you'll see a lot of cursed code. Okaaay, let's go. Well, why do I raise the question? If a common CG code bores you, you can skip the next section and scroll straight to the last picture.

We published and translated this article with the copyright holder's permission. The article was originally published on Habr.
The author is Dmitry Sokolov, a programmer whose hobby and profession are computer graphics and geometry. GitHub: ssloy.
So, I promised to write a simple yet quite complete compiler for the wend language that I just invented over the weekend. Although it's easy to write, it's harder to describe. A good description needs vibrant examples. I'm allergic to code examples like calculating Fibonacci numbers. For crying out loud! Since wend is pretty primitive, I need examples that are simple yet still impressive. Suddenly, remembered the old demoscene! Let's say, I want a bonfire rendering.
It's not that difficult: I can't run graphics mode, but my console supports the \033[ escape sequence, so a single print instruction is enough to draw the fire! By the way, I've heard that the Windows console supports the ANSI escape sequences, but I haven't checked it myself.
The technology being sorted out, all that's left to do is write the code. Since I am only half-crazy, I'll write it first in C, and then translate it (manually) into the wend language. Indeed, my compiler is good, but C offers a greater variety of tools. Plus, my compiler isn't bug-free, and I'm too lazy to ferret out these issues. I've come across the GCC bugs before, of course, but they're rare and almost extinct.
Let's see how to create such a fire, and then we'll get back to the preprocessor and black magic. This is what the necessary wrapper looks like:
#include <stdio.h>
#include <stdint.h>
#include <stdlib.h>
#include <unistd.h>
#define WIDTH 80
#define HEIGHT 25
#define FPS 30
const char* palette[256] = {
#define ANSIRGB(R,G,B) "\033[48;2;" #R ";" #G ";" #B "m "
ANSIRGB( 0, 0, 0), ANSIRGB( 0, 4, 4),
ANSIRGB( 0, 16, 20), ANSIRGB( 0, 28, 36),
ANSIRGB( 0, 32, 44), ANSIRGB( 0, 36, 48),
ANSIRGB( 60, 24, 32), ANSIRGB(100, 16, 16),
ANSIRGB(132, 12, 12), ANSIRGB(160, 8, 8),
ANSIRGB(192, 8, 8), ANSIRGB(220, 4, 4),
ANSIRGB(252, 0, 0), ANSIRGB(252, 0, 0),
ANSIRGB(252, 12, 0), ANSIRGB(252, 28, 0),
ANSIRGB(252, 40, 0), ANSIRGB(252, 52, 0),
ANSIRGB(252, 64, 0), ANSIRGB(252, 80, 0),
ANSIRGB(252, 92, 0), ANSIRGB(252, 104, 0),
ANSIRGB(252, 116, 0), ANSIRGB(252, 132, 0),
ANSIRGB(252, 144, 0), ANSIRGB(252, 156, 0),
ANSIRGB(252, 156, 0), ANSIRGB(252, 160, 0),
ANSIRGB(252, 160, 0), ANSIRGB(252, 164, 0),
ANSIRGB(252, 168, 0), ANSIRGB(252, 168, 0),
ANSIRGB(252, 172, 0), ANSIRGB(252, 176, 0),
ANSIRGB(252, 176, 0), ANSIRGB(252, 180, 0),
ANSIRGB(252, 180, 0), ANSIRGB(252, 184, 0),
ANSIRGB(252, 188, 0), ANSIRGB(252, 188, 0),
ANSIRGB(252, 192, 0), ANSIRGB(252, 196, 0),
ANSIRGB(252, 196, 0), ANSIRGB(252, 200, 0),
ANSIRGB(252, 204, 0), ANSIRGB(252, 204, 0),
ANSIRGB(252, 208, 0), ANSIRGB(252, 212, 0),
ANSIRGB(252, 212, 0), ANSIRGB(252, 216, 0),
ANSIRGB(252, 220, 0), ANSIRGB(252, 220, 0),
ANSIRGB(252, 224, 0), ANSIRGB(252, 228, 0),
ANSIRGB(252, 228, 0), ANSIRGB(252, 232, 0),
ANSIRGB(252, 232, 0), ANSIRGB(252, 236, 0),
ANSIRGB(252, 240, 0), ANSIRGB(252, 240, 0),
ANSIRGB(252, 244, 0), ANSIRGB(252, 248, 0),
ANSIRGB(252, 248, 0), ANSIRGB(252, 252, 0),
#define W ANSIRGB(252,252,252)
W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W,
W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W,
W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W,
W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W,
W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W,
W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W,
W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W,
W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W
#undef W
#undef ANSIRGB
};
static uint8_t fire[WIDTH * HEIGHT];
int main() {
printf("\033[2J"); // clear screen
for (;;) {
printf("\033[H"); // home
// rendering body
{
fire[rand()%(WIDTH*HEIGHT)] = 255;
}
for (int j = 0; j<HEIGHT; j++) { // show the buffer
for (int i = 0; i<WIDTH; i++)
printf(palette[fire[i+j*WIDTH]]);
printf("\033[49m\n");
}
usleep(1000000/FPS);
}
return 0;
}First, I define the dimensions of my console (80x25), then define the 256-color palette array and the fire buffer that actually contains the picture of the (future) fire. Then, in the infinite for(;;) loop, I render the buffer, where I fill randomly selected pixels with white color. We get quite an expected result:
The white pixels will be sparks of flame. The sparks cool down pretty quickly while heating the surroundings. It's easy to simulate: at each new frame, we just blur the picture from the previous frame. All the code changes will occur inside the block marked as // rendering body, so I won't provide entire code samples. You can find the final code in my compiler repository. The simplest way to blur the picture is to compute the average value of each pixel in relation to its neighboring pixels. Almost all implementations I come across require creating a copy of the entire buffer. Look it up yourself on Wikipedia. At the same time, such filters are separable by coordinates, so the blur is fully equal to two motion blur filters: one horizontal and the other vertical. Let's start with the vertical one:
void line_blur(int offset, int step, int nsteps) {
uint8_t circ[3] = {0, fire[offset], fire[offset+step]};
uint8_t beg = 1;
for (int i=0; i<nsteps; i++) {
fire[offset] = (circ[0]+circ[1]+circ[2])/3;
circ[(beg+++2)%3] = i+2<nsteps ? fire[offset+2*step] : 0;
offset += step;
}
}
int main() {
[...]
// rendering body
{
// box blur: first horizontal motion blur then vertical motion blur
for (int j = 0; j<HEIGHT; j++)
here -> line_blur(j*WIDTH, 1, WIDTH);
fire[rand()%(WIDTH*HEIGHT)] = 255;
}
[...]
}I think a three-element ring buffer is all we need: no more copies of the screen buffer. The code outputs the following result (I slowed down the video a bit to make it clearer):
Let's add the horizontal one to it:
// rendering body
{
// box blur: first horizontal motion blur then vertical motion blur
here -> for (int j = 0; j<HEIGHT; j++)
line_blur(j*WIDTH, 1, WIDTH);
for (int i = 0; i<WIDTH; i++)
line_blur(i, WIDTH, HEIGHT);
fire[rand()%(WIDTH*HEIGHT)] = 255;
}
[...]
}The heat from a single pixel quickly spreads over a larger area, so it becomes nearly invisible in my palette. On the first iteration, the white pixel is surrounded by eight black pixels; on the second, all nine pixels have a value of 255/9 = 28, and so on:
iteration 1 iteration 2 iteration 3
0 0 0 0 0 3 6 9 6 3
0 0 0 0 28 28 28 0 6 12 18 12 6
0 255 0 0 28 28 28 0 9 18 28 18 9
0 0 0 0 28 28 28 0 6 12 18 12 6
0 0 0 0 0 3 6 9 6 3Here, I scattered sparks all over the screen, but in reality, the heat is coming directly from the fire. Let's fix the code a bit to allow fire pixels to be generated only on the bottom line:
// rendering body
{
// box blur: first horizontal motion blur then vertical motion blur
for (int j = 0; j<HEIGHT; j++)
line_blur(j*WIDTH, 1, WIDTH);
for (int i = 0; i<WIDTH; i++)
line_blur(i, WIDTH, HEIGHT);
for (int i = 0; i<WIDTH; i++) { // add heat to the bed
int idx = i+(HEIGHT-1)*WIDTH;
if (!(rand()%32))
here -> fire[idx] = 128+rand()%128; // sparks
}
}The picture becomes less interesting, but the sky doesn't warm up. We forgot about convection! Let's just scroll the previous frame up one line at each step:
// rendering body
{
here -> for (int j = 1; j<HEIGHT; j++) // scroll up
for (int i = 0; i<WIDTH; i++)
fire[i+(j-1)*WIDTH] = fire[i+j*WIDTH] ;
// box blur: first horizontal motion blur then vertical motion blur
for (int j = 0; j<HEIGHT; j++)
line_blur(j*WIDTH, 1, WIDTH);
for (int i = 0; i<WIDTH; i++)
line_blur(i, WIDTH, HEIGHT);
for (int i = 0; i<WIDTH; i++) { // add heat to the bed
int idx = i+(HEIGHT-1)*WIDTH;
if (!(rand()%32))
fire[idx] = 128+rand()%128; // sparks
}
}That's much better! But our campfire has embers: sparks don't come out of nowhere. Let's paint this place a permanent color (and thus add heat) to the bottom line of the picture:
// rendering body
{
for (int j = 1; j<HEIGHT; j++) // scroll up
for (int i = 0; i<WIDTH; i++)
fire[i+(j-1)*WIDTH] = fire[i+j*WIDTH] ;
// box blur: first horizontal motion blur then vertical motion blur
for (int j = 0; j<HEIGHT; j++)
line_blur(j*WIDTH, 1, WIDTH);
for (int i = 0; i<WIDTH; i++)
line_blur(i, WIDTH, HEIGHT);
for (int i = 0; i<WIDTH; i++) { // add heat to the bed
int idx = i+(HEIGHT-1)*WIDTH;
if (!(rand()%32))
fire[idx] = 128+rand()%128; // sparks
else
here -> fire[idx] = fire[idx]<16 ? 16 : fire[idx]; // ember bed
}
}It's almost good, but too much heat, don't you think? Let's add a cooling effect as a final touch:
// rendering body
{
for (int j = 1; j<HEIGHT; j++) // scroll up
for (int i = 0; i<WIDTH; i++)
fire[i+(j-1)*WIDTH] = fire[i+j*WIDTH];
// box blur: first horizontal motion blur then vertical motion blur
for (int j = 0; j<HEIGHT; j++)
line_blur(j*WIDTH, 1, WIDTH);
for (int i = 0; i<WIDTH; i++)
line_blur(i, WIDTH, HEIGHT);
for (int i = 0; i< WIDTH*HEIGHT; i++) // cool
if (rand()%2 && fire[i]>0)
here -> fire[i]--;
for (int i = 0; i<WIDTH; i++) { // add heat to the bed
int idx = i+(HEIGHT-1)*WIDTH;
if (!(rand()%32))
fire[idx] = 128+rand()%128; // sparks
else
fire[idx] = fire[idx]<16 ? 16 : fire[idx]; // ember bed
}
}Well, that's it. The mundane, non-cursed flame is lit. Let's look at it once again:
I think we're ready to start translating the code to wend, right? Get ready a machina just around the corner, deus ex parked it for me.
The attentive reader might have noticed that in this demo, I fully rendered it in the fire[] array. However, my wend language doesn't have arrays! I can't render pixels separately because the heat dissipation (and convection, too) requires the state of neighboring pixels to be known. However, that's not a problem: I have functions. Let's imagine that I need an 8-element array. We can emulate it using eight different variables and two functions, the getter/setter:
uint8_t fire0, fire1, fire2, fire3, fire4, fire5, fire6, fire7;
uint8_t get_fire(int i) {
if (i==0) return fire0;
if (i==1) return fire1;
if (i==2) return fire2;
if (i==3) return fire3;
if (i==4) return fire4;
if (i==5) return fire5;
if (i==6) return fire6;
if (i==7) return fire7;
}
void set_fire(int i, uint8_t v) {
[...]
}I won't describe the setter because it's structurally similar to the getter. The code seems trivial, but I've just made a linked list instead of an array. To get to the 2,000th element, I'll have to do 2,000 comparisons. With this data size it does not really matter, but I am uneasy. We can use a dichotomy to convert linear complexity to logarithmic.
uint8_t get_fire(int i) {
if (i<4) {
if (i<2) {
if (i<1) {
return fire0;
} else {
return fire1;
}
} else {
if (i<3) {
return fire2;
} else {
return fire3;
}
}
} else {
if (i<6) {
if (i<5) {
return fire4;
} else {
return fire5;
}
} else {
if (i<7) {
return fire6;
} else {
return fire7;
}
}
}
}It's better. This very code pushes me to write the article. How can I create the function? Manually? No way :)
My language is pretty similar to C, so if we write a C code, we can test it properly first and then translate it into the the wend language source code.
My console is 80x25, so I need 2,000 memory cells. 2,048 is very close to 2,000, and it's an exact power of two. So, we get a minimal overhead and don't have to puzzle over about boundary conditions—we can just write a fully-balanced binary search tree. I could have taken any programming language and generated the right text line. However, I don't know why, but I decided to write a simple #define switch in the source code of fire. This #define might switch between a base array and a substitute array: it would have been an easy way to make sure I didn't mess up anywhere. Now I ask myself: can this function be created using the C preprocessor?
To do that, I'd have to write a recursive #define. Is it possible to do this, and if so, how? Of course, I started googling the question. And I accidentally stumbled upon a curious thread on cplusplus.com, I've even screenshoted it.
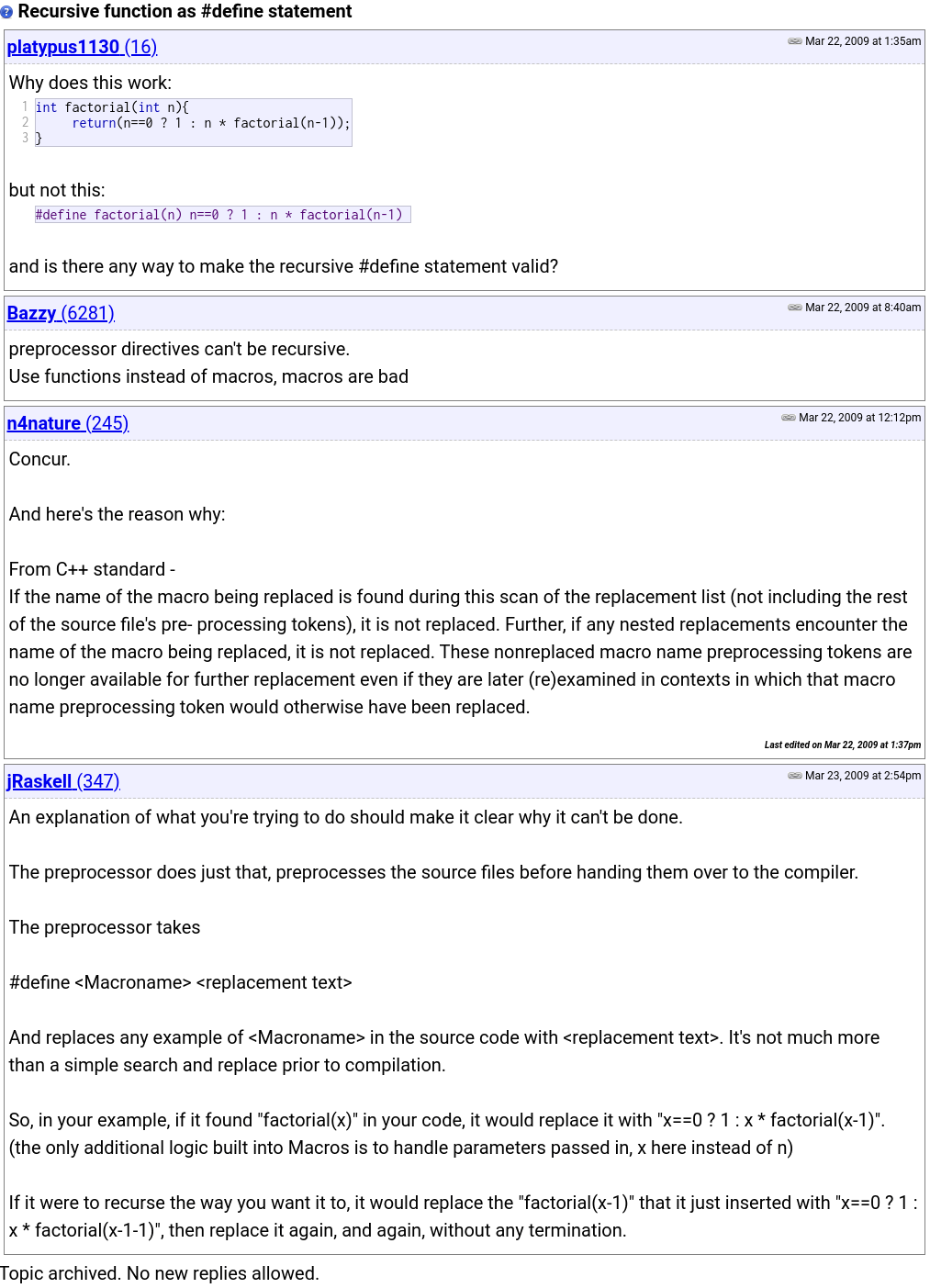
My colleague asked the same question I did. In response, he was told three times that the define recursion was impossible. He. He-he...
Keep in mind that I'm not the smartest person in the room. I just found the right link to Stack Overflow and only tried to sum up what I have learned.
Let's dig into how the C preprocessor works. In the above code (fire), we've already encountered the #define WIDTH 80. This is quite a standard case to define constants. Note: don't do this in C++, constexpr is a better option! Define-s have many unpleasant moments, which can be removed with constexpr. When the lexer encounters the WIDTH token, it replaces it with 80 before running the compiler. Macro commands can also be like functions. For example, the famous #define MIN(X, Y) (((X) < (Y)) ? (X) : (Y)) macro. Note: don't do it like that! In the third decade of the 21st century, I don't see any reason to continue using code from the 70s.
The "execution," or rather the extension of macro commands, is purely textual. The preprocessor doesn't understand the C language. So, if you give it MIN(habracadabra, circ][(beg+++)), it'll happily convert it to (((habracadabra) < (circ][(beg+++))) ? (habracadabra) : (circ][(beg+++)! Check it yourself with gcc -E source.c.
When we want to use a function-like macro command, and we see the similar syntax, most programmers assume that it works like a function too. This means that we first evaluate the parameter values and then pass in the body of the parent macro command. Often, resembles, but not always. The preprocessor isn't the C language, and macros don't behave that way—the example with MIN is proof of that.
Let me give a guide for expanding macro commands in the order in which they're executed:
Let's look at the simplest example of tail recursion (in C):
void recursion(int d) {
printf("%d ", d);
if (d!=0) recursion(d - 1);
}If we call recursion(3), the screen will display 3 2 1 0. We need to learn how to do something like that using only macros. OK, let's go through the ingredients one by one, starting with the simplest and working our way up. We need to know:
Let's start with the first one—how to decrement. The preprocessor is pretty silly. It just replaces text. This may be annoying, but it also allows you to manipulate parts of expressions if you want to. So, it makes a certain sense.
The preprocessor doesn't know anything about arithmetic. It just makes text substitutions, which make things a bit tricky. Let's make the first try:
ssloy@home:~$ gcc -P -E - <<<'
#define DEC(n) n – 1
DEC(3)
'
3 - 1Just to make things clear, I'll run GCC directly on the code from the command line, so you can see both the code and the preprocessor output. So, the DEC(3) macro command doesn't expand into the desired constant, 2, but into the 3-1 expression.
No problem, let's be crafty and use the token concatenation.
ssloy@home:~$ gcc -P -E - <<<'
#define DEC(n) DEC_##n
#define DEC_0 0
#define DEC_1 0
#define DEC_2 1
#define DEC_3 2
DEC(3)
DEC(DEC(3))
'
2
DEC_DEC(3)When we expand DEC(3), the DEC_ and 3 tokens are merged, and a new DEC_3 token is created, which is expanded to 2. Perfect! However, the trick doesn't work with DEC(DEC(3)). Why? That's why I've listed the rules of macro expansion. Concatenation occurs prior to parameters expansion, so the code actually doesn't do what it looks like at first glance: we merge the DEC_ token with the non-expanded text of the DEC(3) parameter, and that's where it stops working. No biggies, it's not too hard to help here: we can just hide the concatenation one level deeper:
ssloy@home:~$ gcc -P -E - <<<'
#define CONCAT(a,b) a##b
#define DEC(n) CONCAT(DEC_,n)
#define DEC_0 0
#define DEC_1 0
#define DEC_2 1
#define DEC_3 2
DEC(3)
DEC(DEC(3))
DEC(DEC(DEC(3)))
> '
2
1
0I declare CONCAT, the macro command to merge two tokens, and all problems disappear: decrement operates fine using numeric constants, not expressions. Note: I can't decrement, for example, 4 in this code. It's fair to ask whether reasonable to define a macro command for each numeric value. Short answer: forget about reason when programming without a parser! The detailed answer: in this case, the decrement is based on the depth of recursion. It seldom goes over a dozen or two levels.
So, we've learned the most important thing—now we can create new tokens by merging pieces, and we can use these tokens as names for other macro commands! In such a case, branching wouldn't be difficult. Let's take a look at the following code:
ssloy@home:~$ gcc -P -E - <<<'
#define IF_ELSE(b) CONCAT(IF_,b)
#define IF_0(i) ELSE_0
#define IF_1(i) i ELSE_1
#define ELSE_0(e) e
#define ELSE_1(e)
IF_ELSE(1)(then body)(else body)
IF_ELSE(0)(then body)(else body)
'
then body
else bodyIF_ELSE is a macro command that takes only 0 or 1 as an argument and generates either the IF_0 token or the IF_1 token using trivial concatenation. IF_0 is a command that generates the ELSE_0 token—it discarding its own arguments along the way. ELSE_0 is just an identity map. Let's follow the whole chain of expanding IF_ELSE(0)(then body)(else body):
IF_ELSE(0)(then body)(else body)
IF_0(then body)(else body)
ELSE_0(else body)
(else body)The expanding with the 1 argument is pretty similar.
Now you're experienced metaprogrammers, tempered like a sword, and won't be scared of a simple null check :)
ssloy@home:~$ gcc -P -E - <<<'
#define SECOND(a, b, ...) b
#define TEST(...) SECOND(__VA_ARGS__, 0)
#define ISZERO(n) TEST(ISZERO_ ## n)
#define ISZERO_0 ~, 1
ISZERO(0)
ISZERO(3)
'
1
0Let's get into it. When we expand ISZERO(n), the first thing we do (again, look at the expansion rule order) is concatenation. In this example, I check ISZERO(0) and ISZERO(3). In the second case, I generate the ISZERO_3 token, but in the first case, I generate ISZERO_0, the name of an already existing macro command! It expands to a list of ~,1. This is the key idea: to get something with a comma, we should pass null to the ISZERO command. If we pass any other number, the result will be an inexisting token.
The rest of the work is handled by the SECOND variadic macro command, which returns its second argument. We know for sure that it'll get at least two arguments as input: ISZERO(3) is expanded into SECOND(ISZERO_3, 0), which equals 0. Well, ISZERO(0) expands to SECOND(~,1,0) and reduces to 1. The tilde character ~ isn't a magic command; it's just a random piece of text because it may create a syntax error when a bug occurs in our macros.
So, we've learned how to decrement, and we've learned how to branch the code by zero. Last leap—let's go! If you've defeated the null check, it means that only the sky is the limit for you.
It's very important to know that all substitutions in macros happen during the lexer execution BEFORE we run a parser. Overall, it's to the parser to handle recursions (hello, Turing completeness in templates). The lexer creators have done a lot to prevent recursive calls.
This is needed to prevent infinite recursion when we expand macros. For example, let's take a look at a case like this:
ssloy@home:~$ gcc -P -E - <<<'
#define FOO F BAR
#define BAR B FOO
FOO
BAR
'
F B FOO
B F BARIt works like this: the preprocessor knows which macros it expands. If it detects one of the macros again at the expanding stage, it paints it blue (the compiler jargon) and leaves it as it is.
Let's suppose we want to expand the FOO token. The preprocessor enters the "expanding FOO" state, processes the F token. However, when it expands the BAR macro, it encounters the FOO token again and immediately marks it, banning further expansion. It's pretty much the same story when we expand the BAR macro.
Now let's cheat a little bit!
ssloy@home:~$ gcc -P -E - <<<'
#define FOO() F BAR
#define BAR() B FOO
FOO()()()()()()()()()
'
F B F B F B F B F BARInteresting and curious. So, what happened? Something pretty interesting happened: we expanded the FOO macro command to a command with parameters. Let's examine two levels of recursion:
FOO()()()()()()()()()
F BAR()()()()()()()()
F B FOO()()()()()()() <- there's a non-blueprinted FOO!When we see FOO for the second time, the lexer doesn't detect it because the lexer generated the FOO token without parameters. That is the end of the FOO handling. Then the lexer continues working, detects the brackets, and calls FOO for the second time. And then a third time. A fourth time.
We're getting lucky!
I remind you that a direct call to FOO() inside BAR doesn't work. We should stop the context of an expanding macro command before we encounter the same macro command token with parameters. And, as it turns out, it's not hard to do. First, let's add an empty macro command, EMPTY():
ssloy@home:~$ gcc -P -E - <<<'
#define EMPTY()
#define FOO() F BAR EMPTY() ()
#define BAR() B FOO EMPTY() ()
FOO()
#define EVAL(x) x
EVAL(FOO())
EVAL(EVAL(FOO()))
EVAL(EVAL(EVAL(FOO())))
EVAL(EVAL(EVAL(EVAL(FOO()))))
'
F BAR ()
F B FOO ()
F B F BAR ()
F B F B FOO ()
F B F B F BAR ()Now, when we try to expand FOO(), the lexer creates the F token and the BAR token that don't match the name of the BAR() macro command. Then the lexer handles the empty token and leaves the brackets () as is. That's it, the FOO() context is done, and nothing has been painted blue. However, FOO() expands to a rather boring F BAR (), just like before. What do we get? Look further down the code. I define the identity macro command #define EVAL(x) x, and the EVAL(FOO()) recursion becomes much more interesting. Let's follow the whole chain (refresh your memory of the expansion rules, especially the last one):
EVAL(FOO()) <- enter the EVAL context
FOO() <- at this stage, the EVAL parameter tokens are recursed
F BAR () <- the single EVAL parameter recursed
F B FOO () <- RESCAN after EVAL parameters have been recursed!Well, that's about it. After wrapping it up in two EVALs, we're done here. In general, we need about as many EVAL wrappers as there are levels of recursion. This can be provided with just a few lines of code. Let's put it all together. Note that we need to get something similar to the C code but with macro recursion!
ssloy@home:~$ gcc -xc - <<<'
#include <stdio.h>
void foo(int d) {
printf("%d ", d);
if (d!=0) foo(d - 1);
}
int main() {
foo(3);
return 0;
}
' && ./a.out
3 2 1 0 ssloy@home:~$No problem at all! Here are just copy-pasted code snippets. We have to be careful with another level of delay on line 29. The BAR token is generated inside the branching instruction, so we need to wait for one more iteration of EVAL to ensure that BAR isn't blueprinted.
ssloy@home:~$ gcc -xc - <<<'
#include <stdio.h>
#define CONCAT(a,b) a##b
#define DEC(n) CONCAT(DEC_,n)
#define DEC_0 0
#define DEC_1 0
#define DEC_2 1
#define DEC_3 2
#define IF_ELSE(b) CONCAT(IF_,b)
#define IF_0(i) ELSE_0
#define IF_1(i) i ELSE_1
#define ELSE_0(e) e
#define ELSE_1(e)
#define SECOND(a, b, ...) b
#define TEST(...) SECOND(__VA_ARGS__, 0)
#define ISZERO(n) TEST(ISZERO_ ## n)
#define ISZERO_0 ~, 1
#define EMPTY()
#define FOO(d) \
printf("%d ", d); \
IF_ELSE(ISZERO(d)) \
( ) \
( BAR EMPTY EMPTY() () (DEC(d)) )
#define BAR(d) FOO EMPTY() (d)
#define EVAL(x) EVAL1(EVAL1(EVAL1(x)))
#define EVAL1(x) EVAL2(EVAL2(EVAL2(x)))
#define EVAL2(x) EVAL3(EVAL3(EVAL3(x)))
#define EVAL3(x) x
int main() {
EVAL(FOO(3))
return 0;
}
' && ./a.out
3 2 1 0 ssloy@home:~$Well, you can find the cursed fire sources here. As I promised, the entire frame buffer is stored in a cluster of separate variables; there are no arrays!
The term "Turing-complete" colloquially means that any real general-purpose computer or computer language can approximately simulate the computational aspects of any other real general-purpose computer or computer language. No real system can have infinite memory, but if we neglect the memory limitation, most programming languages are otherwise Turing-complete.
Not only the preprocessor memory is limited, but also the number of token rescanning levels (which we set with EVAL). However, it's just a form of memory limitation, so the preprocessor is quite Turing-complete.
After I wrote the article, I've found another link to a project where devs have created a programming metalanguage using only defines—it's insane madness. Unfortunately, it's too complicated for the first touch with the b1ack magic of the preprocessor. My tricks can still go into prod, but metalang99's tricks—I doubt it :)
Modern optimizing compilers may be the most complex and impressive creation of humanity in the field of software engineering. However, that's not magic. An ordinary human brain will tell in a few seconds what the below very trivial code should be compiled into, but GCC will need many exabytes of memory and many years to give the answer.
#define X1(x) X2(x)+X2(x)
#define X2(x) X3(x)+X3(x)
#define X3(x) X4(x)+X4(x)
#define X4(x) X5(x)+X5(x)
#define X5(x) X6(x)+X6(x)
#define X6(x) X7(x)+X7(x)
#define X7(x) X8(x)+X8(x)
#define X8(x) X9(x)+X9(x)
#define X9(x) X10(x)+X10(x)
#define X10(x) X11(x)+X11(x)
#define X11(x) X12(x)+X12(x)
#define X12(x) X13(x)+X13(x)
#define X13(x) X14(x)+X14(x)
#define X14(x) X15(x)+X15(x)
#define X15(x) X16(x)+X16(x)
#define X16(x) X17(x)+X17(x)
#define X17(x) X18(x)+X18(x)
#define X18(x) X19(x)+X19(x)
#define X19(x) X20(x)+X20(x)
#define X20(x) X21(x)+X21(x)
#define X21(x) X22(x)+X22(x)
#define X22(x) X23(x)+X23(x)
#define X23(x) X24(x)+X24(x)
#define X24(x) X25(x)+X25(x)
#define X25(x) X26(x)+X26(x)
#define X26(x) X27(x)+X27(x)
#define X27(x) X28(x)+X28(x)
#define X28(x) X29(x)+X29(x)
#define X29(x) X30(x)+X30(x)
#define X30(x) X31(x)+X31(x)
#define X31(x) X32(x)+X32(x)
#define X32(x) X33(x)+X33(x)
#define X33(x) X34(x)+X34(x)
#define X34(x) X35(x)+X35(x)
#define X35(x) X36(x)+X36(x)
#define X36(x) X37(x)+X37(x)
#define X37(x) X38(x)+X38(x)
#define X38(x) X39(x)+X39(x)
#define X39(x) X40(x)+X40(x)
#define X40(x) X41(x)+X41(x)
#define X41(x) X42(x)+X42(x)
#define X42(x) X43(x)+X43(x)
#define X43(x) X44(x)+X44(x)
#define X44(x) X45(x)+X45(x)
#define X45(x) X46(x)+X46(x)
#define X46(x) X47(x)+X47(x)
#define X47(x) X48(x)+X48(x)
#define X48(x) X49(x)+X49(x)
#define X49(x) X50(x)+X50(x)
#define X50(x) X51(x)+X51(x)
#define X51(x) X52(x)+X52(x)
#define X52(x) X53(x)+X53(x)
#define X53(x) X54(x)+X54(x)
#define X54(x) X55(x)+X55(x)
#define X55(x) X56(x)+X56(x)
#define X56(x) X57(x)+X57(x)
#define X57(x) X58(x)+X58(x)
#define X58(x) X59(x)+X59(x)
#define X59(x) X60(x)+X60(x)
#define X60(x) X61(x)+X61(x)
#define X61(x) X62(x)+X62(x)
#define X62(x) X63(x)+X63(x)
#define X63(x) X64(x)+X64(x)
#define X64(x) x+x
int main() {
return X1(0);
}
0